Ist das interessierende Merkmal in den beiden Populationen normalverteilt, und ist die Arbeitshypothese H0 gültig, so ist die Verteilung der Prüfgrösse bekannt. Sie ist mit den Freiheitsgraden df_A und df_B F-verteilt.

Prüfverteilung

F-Verteilung mit den Freiheitsgraden df_A = (n_A - 1) und df_B = (n_B - 1).

In unserem Fall ergeben sich die folgenden Freiheitsgrade: df_A = 47 und df_B = 56.

Überschreitungswahrscheinlichkeit

Wenn wir die Prüfgrösse (1.1521) in die Prüfverteilung einordnen, so können wir abschätzen, mit welcher Wahrscheinlichkeit dieser Ausprägungsgrad zufällig erreicht oder überschritten wird, wenn die beiden Stichproben aus Populationen mit identischen Varianzen stammen.

Prinzipiell beurteilen wir die Überschreitungswahrscheinlichkeit anhand der üblichen Signifikanzniveaus von 5%, 1% oder 0,1%. Die uns verfügbare Tabelle nennt indessen nur die Grenzwerte für das 5%- und das 1%-Niveau.

Wichtiger Hinweis zur manuellen Bearbeitung des Beispiels: Die Freiheitsgrade unseres Beispiels sind in der Tabelle nicht aufgeführt. Man kombiniert deshalb die Freiheitsgrade, zwischen denen df_B und df_A liegen, und notiert die entsprechenden Grenzwerte in einer Skizze.

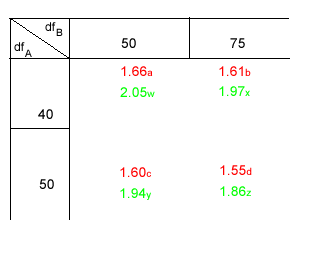
Ausschnitt aus der F-Tabelle

Die tiefgestellten Indizes finden sich auf der Graphik. Sie zeigen an, wo die entsprechenden Grenzwerte zu liegen kommen. Die Farben bezeichnen die Überschreitungswahrscheinlichkeiten.

5%-Grenzwerte: rot

1%-Grenzwerte: grün

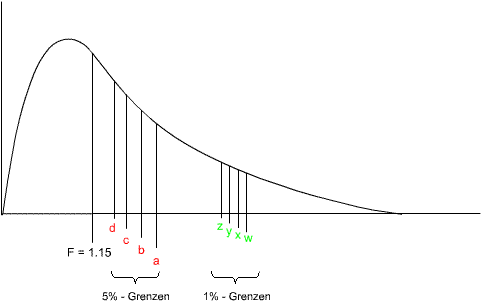
F = 1.1521

Skizze zu den Grenzwerten der Tabelle

Die Skizze zeigt, dass der Ausprägungsgrad der Prüfgrösse kleiner ist als die 5%-Grenzwerte. Damit ist die Überschreitungswahrscheinlichkeit von F=1.15 sicher grösser als 5%. Diese Abschätzung reicht für unsere Zwecke.

In einer realen Untersuchung werden die Berechnungen in der Regel mit einem Statistikprogramm vorgenommen und die Überschreitungswahrscheinlichkeiten exakt bestimmt.

Im nächsten Schritt urteilen wir anhand der Überschreitungswahrscheinlichkeit über Annahme oder Ablehnung der Arbeitshypothese.