Andere Bezeichnungen

Umgangssprachlich: Mittelwert, Durchschnitt

Charakterisierung

Die Summe aller Ausprägungswerte wird durch die Anzahl aller Beobachtungen dividiert.

Bestimmung des arithmetischen Mittelwertes aus den Rohwerten:

Voraussetzungen

Die Addition von Ausprägungsgraden zur Bestimmung des arithmetischen Mittelwertes ist zulässig, wenn das Merkmal mindestens intervall-skaliert ist.

Eignung

Der arithmetische Mittelwert ist die am häufigsten verwendete Kennzahl. Da der arithmetische Mittelwert von allen Ausprägungswerten abhängig ist, kann bei schiefen Verteilungen oder durch einzelne Extremwerte, die für die Verteilung nicht repräsentativ sind, bei kleinen Stichproben ein verzerrter Eindruck entstehen.
Deshalb eignet er sich für eingipflige und symmetrische Häufigkeitsverteilungen sowie für Verteilungen ohne klar erkennbare Konzentration auf einen Ausprägungsgrad. Er eignet sich nicht bei mehrgipfligen und asymmetrischen Verteilungen.

Hinweise und zusätzliche Erklärungen

Unterschiedliche Bezeichnungen des arithmetischen Mittelwertes.

Wenn die Daten aus einer Stichprobenerhebung stammen, wird der arithmetische Mittelwert mit („x-quer“) bezeichnet. Man spricht dabei von einem Verteilungskennwert.
Im Zusammenhang mit Populationen oder theoretischen Verteilungen wird der arithmetische Mittelwert mit („my“) bezeichnet. Wir sprechen von einem Verteilungsparameter.

Berechnung des arithmetischen Mittelwertes aus einer primären oder sekundären Häufigkeitsverteilung

Zu beachten bei Berechnung des arithmetischen Mittelwertes aus einer sekundären Häufigkeitsverteilung

Der aus den Rohwerten oder einer primären Häufigkeitsverteilung berechnete arithmetische Mittelwert kann vom arithmetischen Mittelwert einer sekundären Häufigkeitsverteilung, bei der die Ausprägungsgrade kategorisiert wurden, abweichen, da durch die Kategorisierung Informationen verloren gehen. Es soll darum angegeben werden, auf welchen Datensatz sich der arithmetische Mittelwert bezieht. Nach Möglichkeit soll sich der arithmetische Mittelwert auf die Rohdaten oder die primäre Häufigkeitsverteilung beziehen.

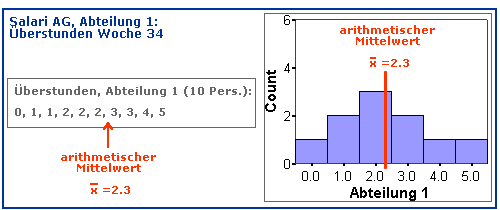
Beispiel: Ermittlung des arithmetischen Mittelwertes aus den Rohwerten und aus einer sekundären Häufigkeitsverteilung (Klicken auf die Box schliesst diese wieder.)