Der Einfluss von unsystematischem Nonresponse auf die Schätzung eines Populationsmittelwertes soll anhand der folgenden Computersimulation illustriert werden:

• Es wird eine Verteilung mit bekannten Parametern für eine Population vom Umfang N = 10'000 generiert.
• Die Verteilung von X stelle eine fiktive Einkommensverteilung in der Population dar.

Der Populationsmittelwert von X sei bekannt:

• Wir ziehen nun zunächst 1'000 einfache Zufallsstichproben vom Umfang n = 500 aus der Population und berechnen für jede Stichprobe den Mittelwert von X.
  Auf diese Weise erhält man die Stichprobenkennwerteverteilung, falls kein Nonresponse vorliegt.
• In einem zweiten Schritt wird Nonresponse von zufälliger Natur simuliert. Wie gehen davon aus, dass die Nonresponse-Rate 10% betrage, d.h. für 10% der Beobachtungen liegen keine Informationen bezüglich X vor.
  D.h. wir ziehen nun ebenfalls 1'000 einfache Zufallsstichproben aus der Population, allerdings nur mit dem Umfang n = 450.
  Auf diese Weise erhält man die Stichprobenverteilung, falls zufälliger Nonresponse vorliegt.

In der unteren Grafik ist zum einen die Verteilung von X in der Population dargestellt (links oben). Die unteren beiden Grafiken stellen die Verteilung der Stichprobenmittelwerte ohne beziehungsweise mit Nonreponse dar.

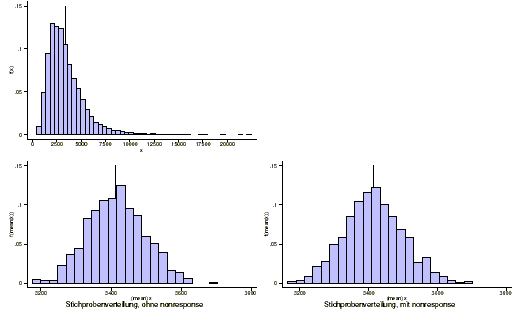
In Bezug auf zufälligen Nonresponse lässt sich das folgende Fazit ziehen:

• Bei zufälligem Nonresponse lässt sich der Populationsmittelwert nach wie vor unverzerrt schätzen.
• Allerdings ist bei zufälligem Nonresponse der Standardfehler der Schätzung grösser, als wenn kein Nonresponse vorliegt.