Der Effekt von Nonresponse auf die Schätzung des Populationsmittelwertes ist gänzlich anders, wenn Nonresponse nicht zufällig, sondern durch einen systematischen Selektionsmechanismus erfolgt.

Zur Illustration wird ebenfalls eine Computersimulation durchgeführt:

• Es wird eine Verteilung mit bekannten Parametern für eine Population vom Umfang N = 10'000 generiert.
• Zunächst wird der Fall simuliert, dass kein Nonresponse vorliegt: Wie ziehen 1'000 einfache Zufallsstichproben vom Umfang n = 500 aus der Population und berechnen für jede Stichprobe den Mittelwert. So erhält man die Stichprobenverteilung ohne Nonresponse.
• Um den Fall von systematischem Nonresponse zu simulieren gehen wir davon aus, dass der folgende Selektionsmechanismus vorliegt. Die Indikatorfunktion I gibt an, ob die Ausprägung von X vorliegt (I=1) oder nicht (I=0).

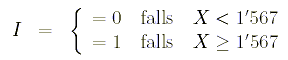
Um nun systematischen Nonresponse zu simulieren, ziehen wir wiederum 1'000 einfache Zufallsstichproben vom Umfang n = 500 aus der Population. Allerdings werden alle Beobachtungen entfernt, welche auf X eine Ausprägung kleiner als 1'567 aufweisen. Danach wird für jede Stichprobe der Mittelwert berechnet. So erhält man die Stichprobenverteilung des Mittelwertes mit Nonresponse.

In der unteren Grafik ist wiederum links oben die Verteilung von X in der Population dargestellt. Die unteren beiden Grafiken stellen die Stichprobenverteilung des Mittelwertes ohne beziehungsweise mit Nonresponse dar.

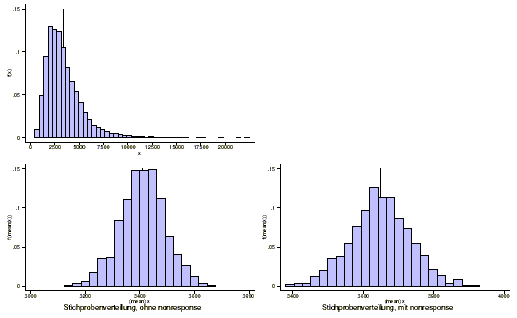
Fazit im Falle von systematischem Nonresponse (s. Grafik):

• Wie im Falle des unsystematischen Nonresponse ist der Standardfehler der Schätzung grösser. Dies ist auf die durch den Nonresponse bedingt Verkleinerung der Stichprobe zurückzuführen.
• Der Populationsmittelwert kann in diesem Fall jedoch ohne Korrektur nicht unverzerrt geschätzt werden.
• Und: Diese Verzerrung ist nicht abhängig von der Stichprobengrösse!