Liegt eine empirisch ermittelte bivariate Verteilung in Form einer Kontingenztafel vor, so kann diese in einfacher Weise mit einer theoretisch erwarteten bivariaten Verteilung verglichen werden. Wie das folgende Beispiel zeigt, stützen wir uns dabei auf das klassische 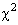-Verfahren.

Unser Interesse gilt der Verteilung der beruflichen Positionen auf die Mitarbeiterinnen und Mitarbeiter in der Euro-Test AG. Für die berufliche Position wurden nur drei Kategorien gewählt so dass die Daten in einer (k×l = 2×3) Kontingenztafel darstellbar sind. In die Tafelzellen eingetragen sind die beobachteten absoluten Häufigkeiten f_bij.

Vor dem Hintergrund der Forderung nach Chancengleichheit der Geschlechter stellt sich die Frage, inwieweit Männer und Frauen in den Kategorien "Oberes Kader", "Mittleres Kader" und "Angestellte" gleich stark vertreten sind.

Zur Untersuchung dieser Frage postulieren wir anhand der Kolonnensummen die bei absoluter Chancengleichheit theoretisch zu erwartende Verteilung: Bei idealer Gleichstellung von Männern und Frauen sind diese in den einzelnen Positions-Kategorien gleichverteilt. So erhalten wir die folgende theoretisch erwartete Verteilung der absoluten Häufigkeiten f_eij:

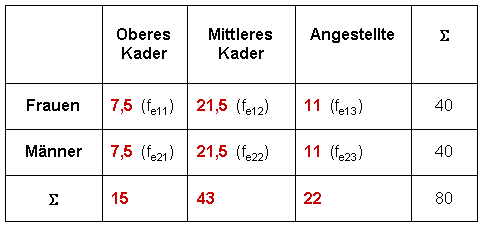
Die empirische und die theoretische Verteilung können wir nun mit dem klassisch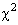en -Verfahren vergleichen. Dabei schätzen wir ab, ob die Unterschiede zwischen den beiden Verteilungen so gravierend sind, dass wir bei der Interpretation der Unterschiede den Zufall mit einer Irrtumswahrscheinlichkeit p < 5% ausschliessen können.

Überlegen Sie sich die für diesen Vergleich notwendigen Arbeitsschritte, bevor Sie zur nächsten Seite übergehen.