Auch der von Kruskal und Wallis entwickelte H-Test basiert auf

1. einer Prüfgrösse,
2. einer Arbeitshypothese H0 und eine Alternativhypothese H1,
3. einer Prüfverteilung, d.h. einer Verteilung, die beschreibt, wie die Prüfgrösse bei Gültigkeit der Arbeitshypothese H0 verteilt ist,
4. einem Signifikanzniveau, das die Beurteilung eines konkret vorliegenden Ausprägungsgrades der Prüfgrösse im Rahmen der Prüfverteilung erlaubt.

Die grundlegende Idee von Kruskal und Wallis, auf der die von ihnen entwickelte Prüfgrösse aufbaut, ist sehr einfach zu verstehen. Wir wollen sie graphisch veranschaulichen.

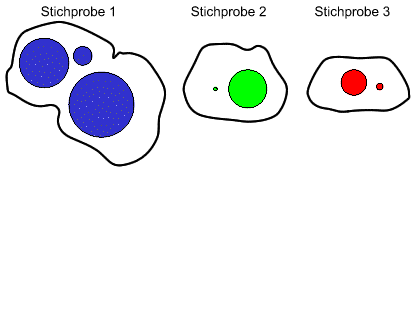
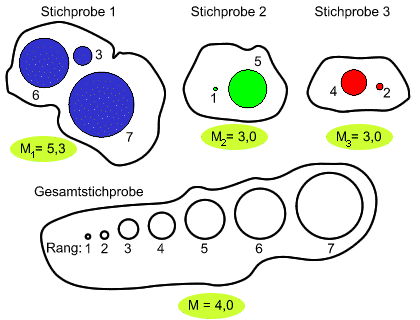
Das folgende Bild zeigt in symbolischer Form drei Stichproben unterschiedlicher Grösse und in jeder Stichprobe die Ausprägungen eines ordinal skalierten Merkmals. Die Daten in den drei Stichproben sind mit unterschiedlichen Farben charakterisiert, damit wir immer wissen, aus welcher Stichprobe sie stammen. Die Grösse der Symbole veranschaulicht den Ausprägungsgrad der Daten.

Wir folgen den Überlegungen von Kruskal und Wallis in einzelnen Schritten:

(0)
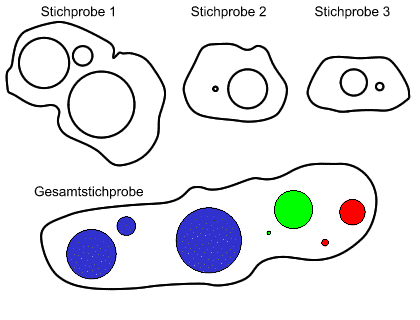
(1)	Als erstes bilden wir eine Gesamtstichprobe, d.h. wir führen die Daten aus allen Stichproben zusammen.
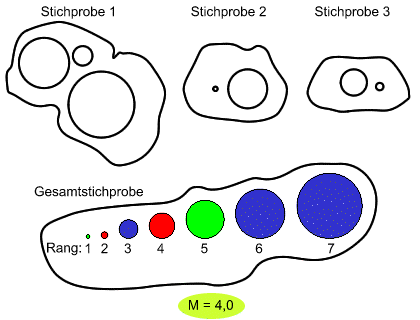
(2)	Dann rangieren wir die Daten in dieser Gesamtstichprobe. Bei den 7 unterschiedlichen Ausprägungen vergeben wir die Ränge 1 bis 7.
(3)	Wie Sie erkennen können, werden die Daten aus den einzelnen Stichproben durchmischt. Für die Gesamtstichprobe ermitteln wir den mittleren Rang M, indem wir die Summe alles vergebenen Ränge durch die Zahl der Daten dividieren.
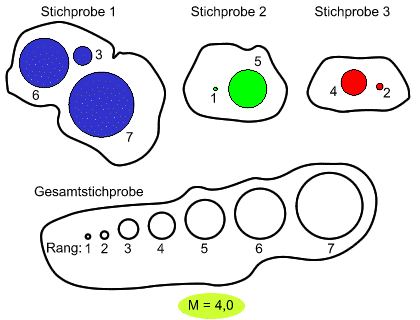
(4)	Nun ordnen wir die Daten wieder in die Stichproben ein, aus denen sie ursprünglich stammten und geben ihnen die Rangplätze mit, die sie in der Gesamtstichprobe erzielten.
(5)	Wir bestimmen für jede Stichprobe den mittleren Rang Mi, indem wir alle Ränge in einer Stichprobe addieren und diese Rangsumme durch die Zahl der Daten in der betreffenden Stichprobe dividieren.

Und nun zum wahrscheinlichkeitstheoretischen Kern der Idee von Kruskal und Wallis, auf den Sie leicht selber kommen könnten.

Stammen die Stichproben bezüglich ihrer zentralen Tendenz aus derselben Population, unterscheiden sie sich also nur zufällig, so müssen sich die in der Gesamtstichprobe erzielten Ränge auch zufällig auf die einzelnen Stichproben verteilen. Oder anders ausgedrückt: In allen Stichproben müssen in vergleichbarer Weise kleine und grosse Rangplätze zu finden sein.