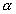Wenn die Stichproben bezüglich der zentralen Tendenz aus derselben Population stammen, so dürfen die mittleren Ränge M₁, M₂,..., M_p der Stichproben nur zufällig vom mittleren Rang M der Gesamtstichprobe abweichen.

Auf der Grundlage dieser Überlegungen haben Kruskal und Wallis eine Prüfgrösse H hergeleitet und bewiesen, dass diese Prüfgrösse H-verteilt ist, wenn die Arbeitshypothese H0 gültig ist. Dass die Definitionsformel dieser Prüfgrösse nicht ganz einfach ist, insbesondere dann, wenn verbundene Ränge vorkommen, haben Sie der Vorbereitungs-Literatur zu diesem Lernschritt entnehmen können.

Da wir für den H-Test in der Regel ein Statistikprogramm einsetzen, verzichten wir an dieser Stelle auf die Wiedergabe der Berechnungsformel.

Nun noch ein Wort zur Prüfverteilung:

Wir wollen p Stichproben mit dem H-Test simultan vergleichen. Sind in mindestens p = 4 Stichproben je mindestens 5 Daten erhoben worden, so geht die H-Verteilung über in ein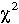e -Verteilung mit dem Freiheitsgrad df = p-1. In allen anderen Fällen müssen wir entweder die spezielle H-Verteilung benutzen, die in Lehrbüchern (z.B. (Bortz et al. 1998)) oder Tabellenwerken nachgeschlagen werden kann, oder wir prüfen, ob die Verteilungen des Merkmals in den hinter den Stichproben stehenden Populationen zumindest ähnlich sind. Auch in diesem, meist nicht leicht zu prüfenden Fall darf anstelle der H-Verteilung die 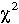-Verteilung (df = p-1) als Prüfverteilung gewählt werden.

Wir machen uns die Sache leicht, wenn wir den H-Test, d.h. Rangvarianzanalysen ohne Messwiederholungen, von SPSS oder einem anderen Statistikprogramm rechnen lassen. SPSS wählt selbständig die adäquate Prüfverteilung und gibt Ihnen direkt die Überschreitungswahrscheinlichkeit der Prüfgrösse aus.

Bevor wir uns dies an einem Beispiel veranschaulichen, stellen wir abschliessend die Elemente des H-Tests nochmals zusammen:

Arbeitshypothese H0 und Alternativhypothese H1:	H0: Die Stichproben stammen aus Populationen, die bezüglich der zentralen Tendenz im interessierenden Merkmal identisch sind. Anders ausgedrückt: Die Stichproben unterscheiden sich bezüglich der zentralen Tendenz des Merkmals nur zufällig. H1: Die Stichproben unterscheiden sich bezüglich der zentralen Tendenz. Prüfen wir auf einen stochastischen Zusammenhang zwischen der unabhängigen Variablen (d.h. dem Definitionsmerkmal der Stichproben) einerseits und der abhängigen Variablen (dem in den Stichproben erhobenen Merkmal) andererseits, so können die Hypothesen auch wie folgt formuliert werden: H0: Zwischen der abhängigen und der unabhängigen Variablen besteht kein statistisch nachweisbarer stochastischer Zusammenhang. H1: Zwischen der abhängigen und der unabhängigen Variablen besteht ein stochastischer Zusammenhang.
Prüfgrösse:	Die Prüfgrösse H bestimmt sich nach der von Kruskal und Wallis hergeleiteten Formel (in diesem Lernschritt nicht wiedergegeben).
Prüfverteilung:	Prüfverteilung ist die H-Verteilung. Die H-Verteilung geht über in eine -Verteilung mit dem Freiheitsgrad df = p-1 (p steht für die Zahl der Stichproben), wenn entweder p 4 und in jeder Stichprobe mindestens 5 Daten erhoben wurden, oder wenn die Verteilungen des Merkmals in den hinter den Stichproben stehenden Populationen ähnlich sind.
Signifikanzniveau:	Wir wählen das Signifikanzniveau, d.h. das -Fehler-Risiko, den Gepflogenheiten entsprechend mit 5%, 1% oder 0,1%.