Soll die beobachtete Verteilung eines intervall- oder proportinal skalierten Merkmals mit einer Normalverteilung verglichen werden, so ist auch dies anhand eines univariaten oder linearen -Verfahrens möglich.

Voraussetzung ist einzig, dass wir angeben können, welche absoluten Häufigkeiten in den einzelnen Ausprägungskategorien theoretisch zu erwarten sind, wenn das Merkmal normalverteilt ist und seine Ausprägungsgrade so kategorisiert werden, wie dies für die beobachteten Ausprägungsgrade gemacht wurde.

Das Verfahren zur Ermittlung dieser theoretischen Verteilung ist formal sehr einfach, die numerische Realisierung aber so aufwendig, dass derartige Vergleiche in der Regel mit einem Statistikprogramm (z.B. SPSS) durchgeführt werden.

So wollen wir uns als erstes auf rein formaler Ebene das Grundprinzip derartiger Vergleiche ansehen und ein konkretes Beispiel dann gleich mit SPSS lösen.

Zur Erläuterung des grundsätzlichen Vorgehens diene uns folgendes Beispiel:

Ein intervall-skaliertes Merkmal wurde in 7 Ausprägungskategorien kategorisiert, als Daten liegen uns die absoluten Häufigkeiten vor, mit denen die 7 Ausprägungskategorien beobachtet wurden. Wir möchten nun prüfen, ob sich diese empirische Verteilung als Ganzes so stark von einer Normalverteilung unterscheidet, dass ausgeschlossen werden kann, dass die Unterschiede zwischen den beiden Verteilungen nur zufällig zustande gekommen sind.

Wollen wir die empirische Verteilung und die theoretisch erwartete Normalverteilung mit einem univariaten -Verfahren vergleichen resp. auf einen signifikanten Unterschied prüfen, so brauchen wir Angaben über die theoretisch erwartete Normalverteilung unseres Merkmals in den gegebenen Ausprägungskategorien.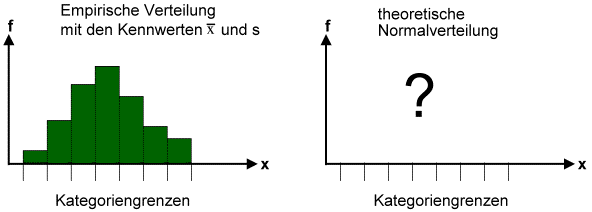



Die theoretischen Häufigkeiten finden wir über das Modell aller Normalverteilungen, über die z-Verteilung, wie folgt:

Als erstes transformieren wir die Kategoriengrenzen der beobachteten Verteilung in die z-Verteilung. Anhand einer z-Tabelle können wir dann die Wahrscheinlichkeiten bestimmen, mit denen der Ausprägungsgrad eines normalverteilten Merkmals in den einzelnen Ausprägungskategorien zu erwarten ist. Diese Wahrscheinlichkeiten entsprechen - Sie erinnern sich - der Fläche unter der z-Funktion zwischen den Kategoriengrenzen.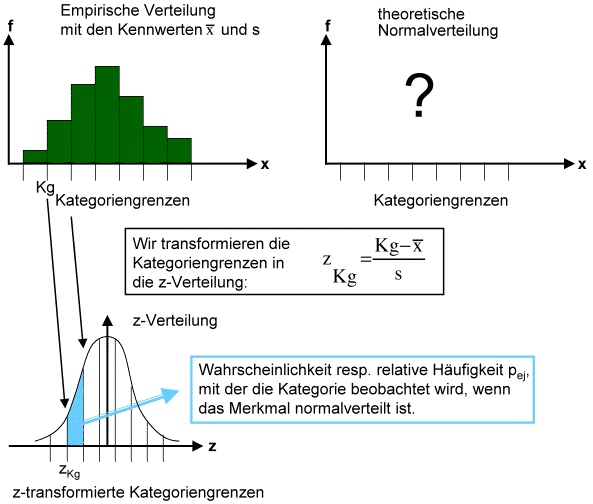



Nun kennen wir die relativen Häufigkeiten, mit denen die einzelnen Ausprägungskategorien zu erwarten sind, wenn das Merkmal normalverteilt ist. Für ein lineares -Verfahren brauchen wir aber die absoluten Häufigkeiten der theoretischen Verteilung. Diese bestimmen wir einfach als Produkt der relativen Häufigkeiten der einzelnen Ausprägungskategorien und der Gesamtzahl der beobachteten Fälle n.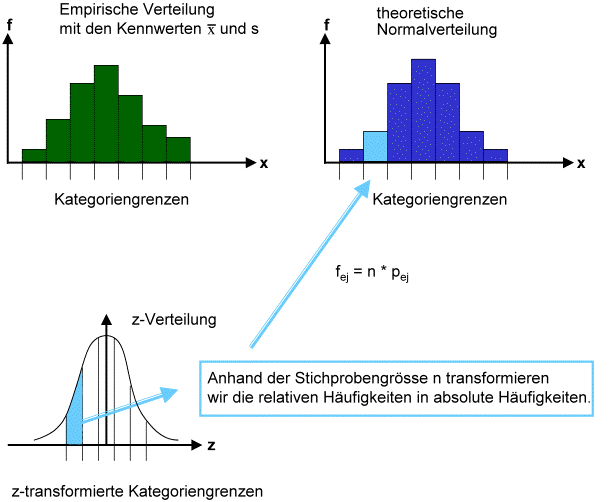



Nun liegt eine empirische und eine theoretisch erwartete Verteilung vor, wir können sie anhand eines linearen Chi-Quadrat-Verfahrens vergleichen. Dazu erinnern wir uns an folgendes:

• Keine der theoretisch erwarteten absoluten Häufigkeiten darf kleiner sein als 5. Ist dies der Fall, so müssen, falls dies aus inhaltlicher Sicht vertretbar ist, benachbarte Ausprägungskategorien zusammengelegt werden. Ein numerisches Beispiel dazu kennen Sie aus der Vorbereitungslektüre.
• Der Freiheitsgrad df der Prüfverteilung ist df = k - 3. Für die theoretische Verteilung gibt es nämlich 3 Vorgaben: Die Zahl der Fälle, den Mittelwert und die Standardabweichung. In unserem konkreten Beispiel umfasst das Merkmal k = 7 Ausprägungskategorien. Prüfverteilung ist also eine -Verteilung mit dem Freiheitsgrad df = 7 - 3 = 4.

Ein 'manueller' Vergleich der beiden Verteilungen mit einem linearen -Verfahren ist nun möglich, rechentechnisch aber so aufwendig, dass wir in der Praxis ein Statistikprogramm (z.B. SPSS) einsetzen. Diese Programme realisieren den gewünschten Vergleich aber meist nicht über ein -Verfahren, sondern anhand verwandter Tests, die andere Prüfgrössen und andere Prüfverteilungen benutzen. Eines der wichtigsten dieser Verfahren ist der Test nach Kolmogorov-Smirnov. Unter der Rubrik "Fallbeispiele" finden Sie ein konkretes, mit SPSS gelöstes Beispiel.