3. Vergleich von zwei empirischen Verteilungen
Unterscheiden sich Gymnasiastinnen und Gymnasiasten bezüglich ihrer Studieninteressen?
In den Abschlussklassen eines Gymnasiums wurden die generellen Studieninteresse erhoben. Die Maturandinnen und Maturanden
hatten dabei anzugeben, an welcher Fakultät sie planten, ihr Studium aufzunehmen.
Da sich das Rektorat des Gymnasiums für geschlechtsspezifische Studien-Präferenzen interessiert, liess der zuständige Prorektor
die Studienwünsche der Frauen und der Männer separat auszählen. Dabei ergaben sich die folgenden Verteilungen:
| Zahl der Männer | Zahl der Frauen | |
|---|---|---|
| Philosophische Fakultät | 22 | 28 |
| Sozialwissenschaftliche Fakultät | 36 | 25 |
| Naturwissenschaftliche Fakultät | 31 | 20 |
| Medizinische Fakultät | 20 | 21 |
| Wirtschaftswissenschaftliche Fakultät | 42 | 28 |
| Rechtswissenschaftliche Fakultät | 17 | 9 |
| Total Wahlen | 168 | 131 |
Die Verteilungen der Studienwünsche der Frauen und der Männer sollen bezüglich eines signifikanten Unterschieds verglichen werden. Dabei gehen wir wie üblich vor:
- Prüfung der Voraussetzungen und Wahl des Prüfverfahrens:
Das bei den Gymnasiastinnen und Gymnasiasten erhobene Merkmal ist der 'Studienwunsch'; dieses Merkmal ist nominal skaliert. Für den Vergleich der Verteilungen dieses Merkmals in der Stichprobe der Männer und der Stichprobe der Frauen kommt nur ein nichtparametrisches Verfahren in Frage, konkret ein lineares Chi-Quadrat-Verfahren für unabhängige Stichproben. Die einzige formelle Voraussetzung, dass keine der absoluten Häufigkeiten kleiner sei als 5, ist im Rahmen dieses Beispiels erfüllt. - Arbeitshypothese H0:
Die beiden Verteilungen unterscheiden sich als Ganzes nur zufällig.
Alternativhypothese H1:
Die beiden Verteilungen unterscheiden sich nicht zufällig. - Als erstes muss entschieden werden, welche der beiden Verteilungen als die 'theoretisch erwartete Verteilung' gelten soll.
Da im Rahmen unseres Beispiels nichts für die eine oder andere Lösung spricht, wählen wir die Verteilung in der Stichprobe
der Maturandinnen als 'theoretisch erwartete Verteilung'.
Dies zeigt sich im SPSS-Befehlssatz dadurch, dass wir die Verteilung der Studienwünsche der Maturandinnen unter EXPCTED eingeben. Die Umrechnung in die 'theoretisch erwartete Verteilung' bei gleichen Stichprobengrössen übernimmt SPSS.
DATA LIST /fak 1 freq 3-4.
WEIGHT BY freq.
VALUE LABELS fak 1 'Philosophische Fak'
2 'Sozialwissenschaftliche Fak'
3 'Naturwissenschaftliche Fak'
4 'Medizinische Fak'
5 'Wirtschaftswissenschaftliche Fak'
6 'Rechtswissenschaftliche Fak' .
BEGIN DATA
1 22
2 36
3 31
4 20
5 42
6 17
END DATA.
NPAR TESTS /CHISQUARE = fak /EXPECTED = 28 25 20 21 28 9.
SPSS output (Klicken auf die Box schliesst diese wieder.)
- Interpretation der Ergebnisse:
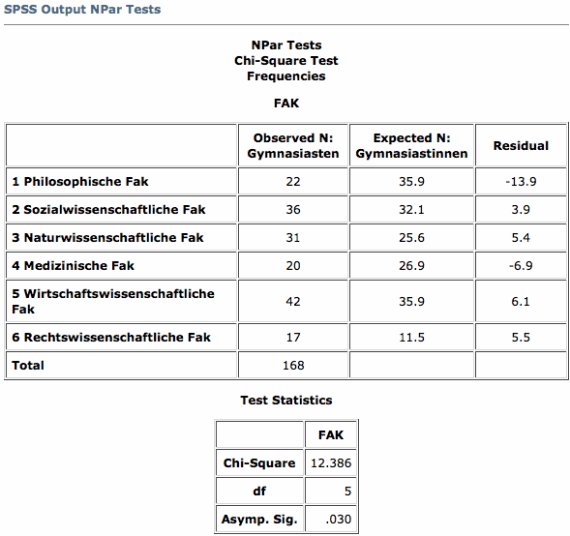
Die SPSS-Ausgabe zeigt uns als erstes die Häufigkeitsverteilung des Merkmals 'Studienwünsche' für die Stichprobe der Maturanden (observed) und die auf die gleiche Stichprobengrösse transformierte 'theoretisch erwartete Verteilung' der Maturandinnen (expected).
Anschliessend wird der Ausprägungsgrad der Prüfgrösse (Chi-Square) und dessen zweiseitige Überschreitungswahrscheinlichkeit ausgegeben. Da dieser kleiner ist als 5%, lehnen wir unsere Arbeitshypothese H0 zu Gunsten von H1 ab.
Inhaltlich bedeutet dies, dass bezüglich der Studienwünsche in den Abschlussklassen dieses Gymnasiums ein geschlechtsspezifischer Unterschied nachgewiesen werden kann.