Eine empirische (beobachtete) Verteilung kann anhand der Prüfgrösse mit jeder beliebigen theoretischen Verteilung verglichen und auf signifikante Unterschiede geprüft werden.

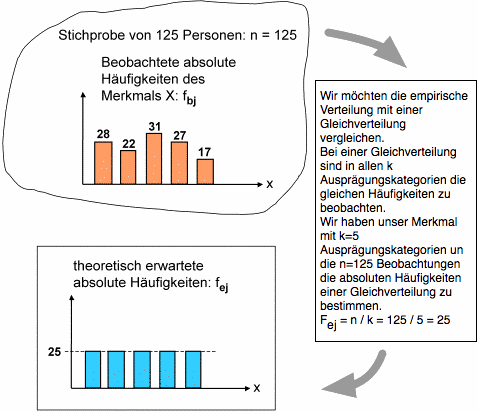
Dabei steht k für die Zahl der Ausprägungskategorien der zu vergleichenden Verteilungen, f_bj für die beobachtete und f_ej für die erwartete absolute Häufigkeit in der j'ten Ausprägungskategorie.

Unter der Voraussetzung, dass kein f_ej (j=1...k), d.h. keine der erwarteten absoluten Häufigkeiten, kleiner ist als 5, ist die Prüfverteilung bekannt: Es ist eine -Verteilung.

Nun gibt es aber eine ganze Familie von -Verteilungen; wir unterscheiden sie anhand des Freiheitsgrades df.

Welche -Verteilung im konkreten Fall als Prüfverteilung dient, ist abhängig von k, der Anzahl Ausprägungskategorien, und von der Art der theoretischen Verteilung, mit der verglichen werden soll.

Auf die formale Herleitung des für jede theoretische Verteilung optimalen Freiheitsgrades df können wir hier nicht eingehen; eine Faustregel deckt uns aber die wichtigsten drei Fälle ab.

Damit wir diese verstehen können, müssen wir kurz überlegen, was als erstes zu tun ist, wenn wir eine beobachtete (empirische) Verteilung mit einer theoretischen Verteilung vergleichen wollen.

Die univariaten (linearen) -Verfahren basieren auf dem Vergleich der beobachteten und der theoretisch erwarteten absoluten Häufigkeiten der Ausprägungskategorien. Dies bedeutet, dass wir die theoretisch erwartete Verteilung für die Kategorien der empirischen Verteilung und die Anzahl der beobachteten Fälle definieren müssen. Auf der Anzahl Ausprägungskategorien (k) und der Zahl der für die theoretische Verteilung notwendigen "Vorgaben" basiert die Einschätzung des Freiheitsgrades der Prüfverteilung.

Unter Anzahl "Vorgaben" soll die Zahl der Stichproben-Kenngrössen (z.B. Stichprobengrösse, Mittelwert etc.) verstanden werden, die zur Bestimmung der theoretischen Verteilung benötigt werden.

Einfaches Beispiel erwünscht? (Klicken auf die Box schliesst diese wieder.)

Betrachten wir die drei wichtigsten Fälle: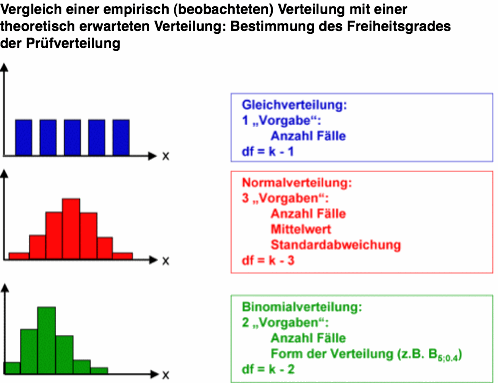



Für diese drei Fälle ist der Freiheitsgrad der Prüfverteilung eindeutig festgelegt. In der Praxis kommen aber auch theoretisch erwartete Verteilungen vor, bei denen bezüglich der Vorgaben ein Interpretationsspielraum besteht. In solchen Fällen wählen wir den höheren Freiheitsgrad und entscheiden bezüglich der Ablehnung unserer Arbeitshypothese H₀ konservativ. In anderen Worten: Bei Unsicherheit fordern wir zwischen der empirischen und der theoretischen Verteilung einen etwas grösseren Unterschied, um die Arbeitshypothese zu verwerfen.

Hinweis: Unter der Rubrik "Fallbeispiele" findet sich ein Beispiel zum Vergleich einer empirischen Verteilung mit einer Gleichverteilung.