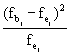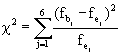1. Vergleich einer empirischen Verteilung mit einer Gleichverteilung

Fallbeispiel 1: Ist Precilla Cornflakes wirklich eine Falschspielerin?

Wir erinnern uns an unsere Einführungsgeschichte. Auf dem Küchentisch von O'Neel liegen zwei Häufigkeitsverteilungen. Die eine zeigt die Häufigkeiten, mit denen die Würfelbilder von Precillas Würfel in 120 Würfen aufgetreten sind. Die andere zeigt die von Pastor Detlev theoretisch erwartete Verteilung dieser Häufigkeiten für einen idealen, nicht präparierten Würfel.

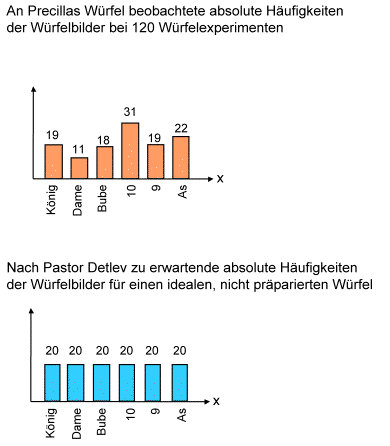
O'Neel und seine Frau Emme stehen vor der Frage, ob sich diese recht unterschiedlichen Verteilungen so stark unterscheiden, dass bei der Erklärung dieses Unterschiedes der Zufall ausgeschlossen werden kann. Wäre dies der Fall, so wäre Precillas Würfel präpariert und Precilla müsste als Falschspielerin ins Kittchen.

Mit unserem Wissen um die -Verfahren können wir O'Neel und Emme bei der Beantwortung dieser Frage behilflich sein. Es geht um den Vergleich einer empirischen Verteilung mit einer Gleichverteilung.

Wir lösen das Problem über die üblichen Arbeitsschritte:

  • Prüfung der Voraussetzungen und Wahl des Prüfverfahrens:
    Es gibt nur ein interessierendes Merkmal: Die Würfelbilder. Dieses Merkmal hat 6 Ausprägungskategorien und ist nominal skaliert. Zudem sollen zwei Verteilungen gesamthaft verglichen und auf einen signifikanten Unterschied geprüft werden: Wir wählen ein univariates -Verfahren.
  • Formulierung der Arbeitshypothese H0 und der Alternativhypothese H1:
    H0: Die beiden Verteilungen unterscheiden sich nur zufällig.
    H1: Die beiden Verteilungen unterscheiden sich nicht nur zufällig.

Ermittlung des Ausprägungsgrades der Prüfgrösse (mittels einer Tabelle) (Klicken auf die Box schliesst diese wieder.)

  • Ermittlung der Prüfverteilung:
    Da wir unsere empirische Verteilung mit einer Gleichverteilung vergleichen, bestimmt sich der Typ der -Verteilung, d.h. der Freiheitsgrad df wie folgt: df = k - 1 = 6 - 1 = 5
  • Ermittlung der Überschreitungswahrscheinlichkeit:
    Die Prüfgrösse hat im gegebenen Fall einen Ausprägungsgrad von 10,6. Bestimmen Sie die Überschreitungswahrscheinlichkeit dieses Ausprägungsgrades anhand der passenden Tabelle.
1. Die Übertretungswahrscheinlichkeit ist
 
 
 
 
2. Die Arbeitshypothese kann damit
 
 

Lösung (Klicken auf die Box schliesst diese wieder.)

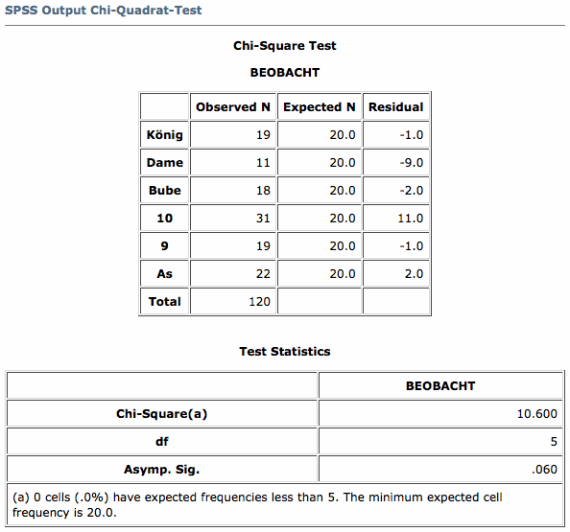
Datenauswertung mit SPSS

Abschliessend wollen wir uns ansehen, wie ein mit SPSS realisierter Vergleich der beiden Verteilungen aussieht. Zu diesem Zweck speichern wir die Resultate der 120 Würfelexperimente von O'Neel als Ausprägungen der Variablen beobacht in einem Datenfile mit dem Namen 'precilla.sav' und geben die folgenden SPSS-Befehle ein:

GET FILE 'X:\\SPSS-DAT\\precilla.sav'.
VALUE LABELS beobacht 1 'König' 2 'Dame' 3 'Bube' 4 '10' 5 '9' 6 'As'.
NPAR TESTS /CHISQUARE = beobacht /EXPECTED = 20 20 20 20 20 20.

Wir lesen das Datenfile 'precilla.sav' und verlangen einen univariaten (linearen) -Test, wobei wir als Vergleichs-Verteilung eine Gleichverteilung definieren (EXPECTED = 20 20 20 20 20 20).

SPSS Output zeigen (Klicken auf die Box schliesst diese wieder.)