Ein lineares -Verfahren kann uns auch dienlich sein, um zwei empirische Verteilungen als Ganzes zu vergleichen. Da dabei nur die Unterschiede in den Häufigkeiten der Ausprägungskategorien ausgewertet werden, ist dies auf allen Skalenniveaus möglich.

Zwei spezielle Sachverhalte, die sich aus der Definition der Prüfgrösse ergeben, müssen beim Vergleich zweier empirischer Verteilungen aber berücksichtigt werden. Wir wollen sie uns im Detail ansehen.

Sie erinnern sich, die Prüfgrösse ist wie folgt definiert: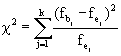

Im Zähler der Summanden stehen die quadrierten Abweichungen zwischen den beobachteten und den erwarteten absoluten Häufigkeiten (f_bj - f_ej)², im Nenner die erwartete absolute Häufigkeit fej. Diese Division durch f_ej normiert die im Zähler stehenden quadrierten Abweichungen so, dass grosse Abweichungen von der theoretisch erwarteten Verteilung stärker gewichtet werden als kleine Abweichungen.

Inhaltlich bedeutet dies, dass die beobachtete Verteilung bezüglich der theoretisch erwarteten Verteilung beurteilt wird. Dies ergibt keine Probleme, solange tatsächlich eine empirische mit einer theoretisch erwarteten Verteilung verglichen wird.

Liegen nun aber zwei empirische, d.h. beobachtete Verteilungen vor, so muss entschieden werden, welche der Verteilungen zur Normierung herangezogen werden soll. In anderen Worten:

Diese Entscheidung, die nur nach inhaltlichen Gesichtspunkten getroffen werden kann, ist bedeutungsvoll. Von ihr hängt der Ausprägungsgrad der Prüfgrösse und damit auch das Ergebnis des Vergleichs der beiden Verteilungen ab.

Der zweite Punkt, der zu beachten ist, betrifft die Tatsache, dass sich die Prüfgrösse auf die absoluten Häufigkeiten abstützt. Dies erfordert, dass die beiden zu vergleichenden Verteilungen eine gleiche Anzahl von Beobachtungen umfassen müssen.

Nun kommt es aber häufig vor, dass die beiden Stichproben, in denen das interessierende Merkmal erhoben wurde, nicht gleich gross sind, womit die beiden zu vergleichenden Verteilungen eine unterschiedliche Anzahl von Beobachtungen beinhalten.

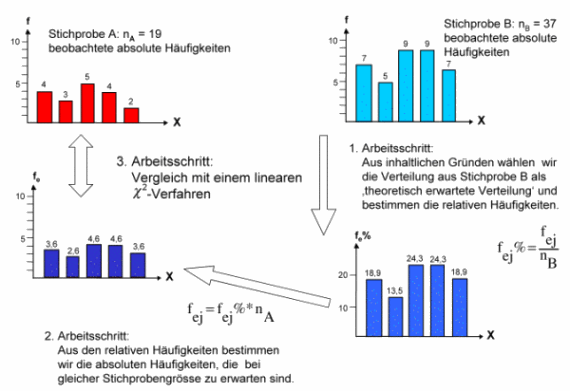
Wir lösen dieses Problem über die folgenden Arbeitsschritte (Klicken auf die Box schliesst diese wieder.)

Wir bestimmen für die gewählte 'theoretisch erwartete Verteilung' die relativen Häufigkeiten. Multiplizieren wir diese relativen Häufigkeiten mit der Stichprobengrösse der anderen Stichprobe, so erhalten wir die 'theoretisch erwarteten absoluten Häufigkeiten' für den Fall, dass die beiden Stichproben gleich gross sind. Jetzt ist ein Vergleich mit einem linearen möglich.

Ein einfaches, mit SPSS gelöstes Beispiel findet sich unter der Rubrik "Fallbeispiele".