Sind die in einer Stichprobe erzielten Testresultate näherungsweise normalverteilt?

Im Rahmen einer Testentwicklung wurde eine Aufgabenserie entworfen, mit der die Fähigkeit zur adäquaten Beurteilung sozialer Situationen eingeschätzt werden soll. In einem ersten Versuch wurde die Aufgabenserie einer Stichprobe von Probandinnen und Probanden vorgelegt, von der angenommen werden darf, dass sie für die Population der 20- bis 21-jährigen deutschsprachigen Mitteleuropäerinnen und Mitteleuropäer einigermassen repräsentativ ist. Die Testresultate der Versuchspersonen, d.h. die Anzahl der als korrekt beurteilten Antworten, wurden als Ausprägungsgrade der Variablen atest1 in einem Datenfile mit dem Namen soz-kom.sav für eine Auswertung mit SPSS gespeichert.

Die Testentwicker möchten die Daten dieses ersten Versuches bezüglich ihrer Verteilung analysieren. Konkret möchten sie wissen, ob angenommen werden darf, dass die von den Versuchspersonen erzielten Resultate näherungsweise normalverteilt sind. Sie bearbeiten diese Fragestellung über die üblichen Arbeitsschritte.

• Prüfung der Voraussetzungen und Wahl des Prüfverfahrens:
  Das interessierende Merkmal ist die Zahl der richtig gelösten Aufgaben; dieses Merkmal ist proportional skaliert. Es soll eine empirische Verteilung mit einer Normalverteilung verglichen werden, wobei die konkrete Fragestellung lautet: Darf angenommen werden, dass die empirische Verteilung der Daten nur zufällig von einer Normalverteilung abweicht?
  Wir wissen, dass diese Frage manuell mit einem linearen -Verfahren, etwas schneller aber mit Hilfe von SPSS und dem Kolmogorov-Smirnov-Test angegangen werden kann
• Arbeitshypothese H₀: Die empirische Verteilung unterscheidet sich von einer Normalverteilung nur zufällig.
  Alternativhypothese H₁: Die empirische Verteilung unterscheidet sich nicht nur zufällig von einer Normalverteilung.
• Datenanalyse mit Hilfe von SPSS und dem Kolmogorov-Smirnov-Test:
  Wir lesen unser Datenfile 'soz-kom.sav' ein, verlangen eine graphische Darstellung der empirischen Häufigkeitsverteilung und vergleichen diese anhand des Kolmogorov-Smirnov-Tests mit einer Normalverteilung. Hierfür wählen wir die folgenden SPSS-Befehle:
  
  GET FILE 'X:\\SPSS-DAT\\soz.kom.sav'.
  FREQUENCIES VARIABLES = atest1 /FORMAT NOTABLE /HISTOGRAMM NORMAL.
  NPAR TEST /K-S (NORMAL) atest1.

SPSS output (Klicken auf die Box schliesst diese wieder.)

• Interpretation der Ergebnisse:
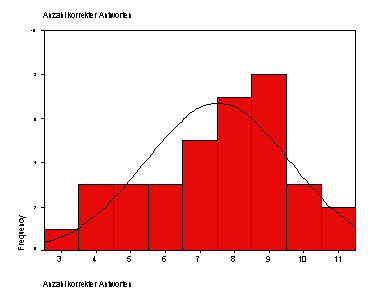
  Die SPSS-Ausgabe zeigt uns als erstes die Häufigkeitsverteilung des Merkmals 'Anzahl korrekter Antworten' für die untersuchte Stichprobe von 35 Versuchspersonen. Für den optischen Vergleich der empirischen Verteilung mit einer Normalverteilung haben wir die Normalverteilung ins Histogramm eintragen lassen.
  
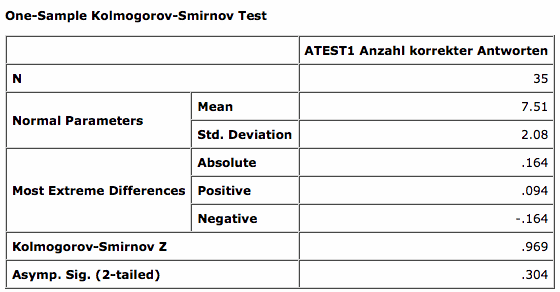
  Als zweites nennt uns SPSS die Kennwerte des Tests nach Kolmogorov-Smirnov, wobei für uns die zweiseitige Überschreitungswahrscheinlichkeit [Asymp. Sig. (2-tailed)] der Prüfgrösse nach Kolmogorov-Smirnov von Bedeutung ist. Diese beträgt 30,4%. Unter Annahme der Gültigkeit der Arbeitshypothese H₀ wird der Ausprägungsgrad der Prüfgrösse also in 30,4% der Fälle zufällig erreicht oder überschritten.
  Da unsere Frage die Annahme der Arbeitshypothese betrifft, beurteilen wir diese Überschreitungswahrscheinlichkeit am 25% -Signifikanzniveau. Da wir mit 30,4% über dem 25%-Niveau liegen, nehmen wir die Arbeitshypothese an und kommen zum Schluss, dass es nicht auszuschliessen ist, dass unsere empirische Verteilung nur zufällig von einer Normalverteilung abweicht. Eine Irrtumswahrscheinlichkeit kann in diesem Fall nicht angegeben werden.
  In der Praxis geht man in dieser Situation davon aus, dass die Stichprobe aus einer Population stammt, in der das interessierende Merkmal normalverteilt ist.