Wie ist nun aber die Prüfgrösse verteilt, wenn die Arbeitshypothese H₀ gültig ist, d.h. wenn sich die beiden Verteilungen nur zufällig unterscheiden?

Die Statistiker verraten uns das Geheimnis.

Für den Vergleich einer beobachteten (empirischen) Verteilung mit einer Gleichverteilung gilt folgendes:
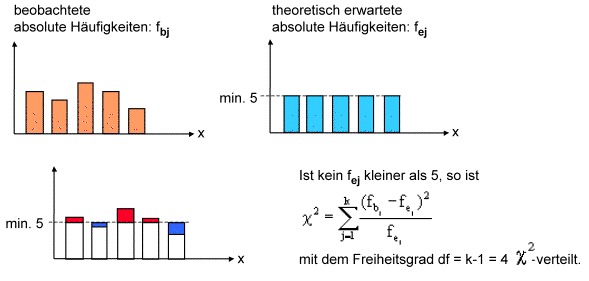
Ist die theoretisch erwartete absolute Häufigkeit f_ej für keine Ausprägungskategorie kleiner als 5, so ist die Prüfgrösse mit dem Freiheitsgrad df (df = k -1) -verteilt.

In unserem Einführungsbeispiel umfassen die beobachtete und die theoretisch erwartete Verteilung k = 5 Ausprägungskategorien. Ist keine der erwarteten absoluten Häufigkeiten f_ej kleiner als 5, so ist die Prüfverteilung eine -Verteilung mit dem Freiheitsgrad df = 4.

Damit haben wir das Grundkonzept aller univariaten (oder linearen) -Verfahren kennengelernt und alles zusammengetragen, was wir für den Vergleich von zwei ganzen Verteilungen brauchen:

• Die Prüfgrösse , die den konkreten Unterschied zwischen den zu vergleichenden Verteilungen beschreibt.
• Eine Arbeitshypothese H₀ (Die beiden Verteilungen unterscheiden sich nur zufällig) und eine Alternativhypothese H₁ (Die beiden Verteilungen unterscheiden sich nicht zufällig).
• Die Prüfverteilung: Unter der Voraussetzung, dass kein f_ej kleiner ist als 5, wissen wir, wie die Prüfgrösse bei Gültigkeit der Arbeitshypothese H₀ verteilt ist.
• Als a-Fehler-Risiko, d.h. als Signifikanzniveau p, akzeptieren wir wie üblich 5%, 1% oder 0,1%.