Den Ausgangspunkt für die Entwicklung einer adäquaten Prüfgrösse haben wir schon gefunden, es sind die in den einzelnen Ausprägungskategorien beobachteten Häufigkeitsunterschiede (f_bj - f_ej).

Da mit der gesuchten Prüfgrösse die beiden Verteilungen gesamthaft verglichen werden sollen, muss sie die Häufigkeitsunterschiede in allen k Ausprägungskategorien umfassen.

Als erstes denken wir natürlich an die Summe der k Häufigkeitsunterschiede, verwerfen die Idee aber schon nach einer kurzen Überlegung:

Da sowohl positive wie auch negative Häufigkeitsunterschiede vorliegen, kann ihre Summe auch bei grossen Unterschieden klein werden (beim Vergleich einer empirischen Verteilung mit einer Gleichverteilung wird die Summe sogar per Definition gleich Null). Positive und negative Unterschiede gleichen sich aus. Wie immer in solchen Fällen, müssen wir die Vorzeichen 'loswerden'. Dies gelingt mathematisch am einfachsten, indem wir die Häufigkeitsunterschiede (f_bj - f_ej) quadrieren. Damit haben wir Beschreibungen der k Häufigkeitsunterschiede, die sicher immer positiv sind.

Nun normieren wir (f_bj - f_ej)2 noch bezüglich fej. Dies bedeutet, dass gleich grosse Differenzen zwischen beobachteten und erwarteten Häufigkeiten je nach erwarteter Häufigkeit verschieden gewichtet werden. Bei kleiner erwarteter Häufigkeit wird der Differenz ein grösseres Gewicht gegeben als bei grosser erwarteter Häufigkeit.

Damit haben wir die gesuchte Prüfgrösse gefunden, es ist das klassische Chi-Quadrat: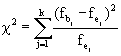

Dabei bedeutet:

• f_bj: beobachtete absolute Häufigkeit der Ausprägungskategorie j
• f_ej: theoretisch erwartete absolute Häufigkeit der Kategorie j
• k: Anzahl Ausprägungskategorien

Nachdem wir eine Prüfgrösse für den Vergleich ganzer Verteilungen gefunden haben, müssen eine diesbezügliche Arbeitshypothese H₀ und eine Alternativhypothese H₁ formuliert werden.

Arbeitshypothese H₀: Die beiden Verteilungen unterscheiden sich nur zufällig.

Alternativhypothese H₁: Die beiden Verteilungen unterscheiden sich nicht zufällig.