Bevor wir die Lösung des gestellten Problemes angehen, erscheint es als sinnvoll, zunächst einige wichtige Definitionen sowie die entsprechende Notation festzuhalten.

• Statistische Einheit / Statistisches Element / Beobachtung:
  Beobachtungen sind die "Träger" der letztlich interessierenden Grössen, der Merkmale / Variablen. In aller Regel handelt es sich dabei in sozialwissenschaftlichen Zusammenhängen um Individuen. Es kann sich dabei allerdings auch um Haushalte, Firmen, Gemeinden, etc. handeln
• Grundgesamtheit / Population / Universum:
  Als Grundgesamtheit bezeichnet man die Menge aller im Hinblick auf die Fragestellung der Studie relevanten Beobachtungen. Je nach Fragestellung variiert somit die zugrundeliegende Population. Es ist deshalb notwendig, die Population nach verschiedenen und insbesondere nach inhaltlichen Abgrenzungskriterien eindeutig zu definieren.
  Werden zu sämtlichen Beobachtungen einer Population Daten erhoben, spricht man von einer Voll- oder Totalerhebung.
  Wird nur für eine Teilmenge der Grundgesamtheit Daten erhoben, spricht man von einer Teil- oder Stichprobenerhebung
• Stichprobe:
  Als Stichprobe bezeichnet man eine Teilmenge aus der Studienpopulation. Im Gegensatz zu einer Vollerhebung werden somit bei einer Stichprobenerhebung nicht für sämtliche Beobachtungen Daten erhoben.
  Im folgenden gehen wir von der Annahme aus, dass eine sogenannte einfache Zufallsstichprobe gezogen wird. Bei dieser Art der Stichprobenziehung hat jedes Element der Population dieselbe positive Wahrscheinlichkeit, Eingang in die konkrete Stichprobe zu finden. Das Ziehen einer einfachen Zufallsstichprobe entspricht dem "Urnenmodell" aus der Wahrscheinlichkeitstheorie: Für jedes einzelne Element liegt jeweils eine Kugel in der Urne, aus welcher zufällig die Beobachtungen gezogen werden.

Anmerkungen zur Notation:

Zur Unterscheidung von Populations- und Stichprobenkennwerten werden die ersten mit griechischen und die zweiten mit lateinischen Buchstaben bezeichnet. In statistischen Untersuchungen interessiert man sich sehr häufig für einzelne Momente der Verteilung eines bestimmten Merkmales. Die folgenden Populationskennwerte (arithmetisches Mittel, Varianz, Anteilswert), welche uns im folgenden weiter beschäftigen werden, haben Sie bereits im Rahmen der deskriptiven Statistik kennen gelernt: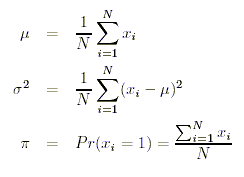

In Analogie zu den Populationkennwerten lassen sich mit Stichprobendaten die folgenden Stichprobenkennwerte berechnen: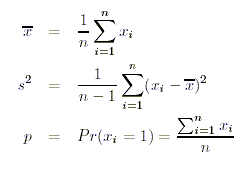

Zentral für das Verständnis dieser Lektion ist der folgende Sachverhalt: Populationskennwerte sind feste (d.h. nicht variable) Grössen, sie sind in aller Regel jedoch unbekannt, weil vollständige Informationen über die Population selten bis nie vorhanden sind. Stichprobenkennwerte hingegen sind als zufällige Grössen aufzufassen, da sie von Stichprobe zu Stichprobe unterschiedlich ausfallen können. Stichprobenkennwerte können damit als das Ergebnis eines Zufallsexperimentes (die Stichprobenziehung) aufgefasst werden. Stichprobenkennwerte sind somit nicht als feste Grössen zu behandeln, sondern als Realisierungen einer Zufallsvariablen.