Es besteht nun allerdings das Problem, dass in aller Regel die Populationsstandardabweichung, welche zur Berechnung des Vertrauensintervalles notwendig ist, unbekannt ist und deshalb ebenfalls anhand der Stichprobendaten geschätzt werden muss.
Man ersetzt deshalb die Populationsstandardabweichung durch die entsprechende Stichprobenstandardabweichung:

Aufgrund der Tatsache, dass die Populationsstandardabweichung aus den vorliegenden Stichprobendaten geschätzt werden muss, gilt, dass die Stichprobenkennwerte nun nicht mehr exakt, sondern nur noch approximativ normalverteilt sind. Diese Approximation gilt ebenfalls nur bei genügend grossem Stichprobenumfang (was als "genügend grosser" Stichprobenumfang gilt, hängt von der Verteilung des Merkmales in der Population ab. Für einen Stichprobenumfang von mehr als 30 Beobachtungen ist die Approximation für praktische Zwecke häufig genügend):

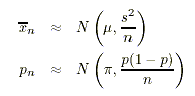
Weil bei grossem Stichprobenumfang die Normalverteilung nach wie vor eine gute Approximation für die Verteilung der Stichprobenkennwerte darstellt, ändert sich nichts Grundlegendes an der Berechnung von Vertrauensintervallen. Man ersetzt nun lediglich die Populationsstandardabweichung durch die entsprechende Schätzung aus den Stichprobendaten. Für den Stichprobenmittelwert ergibt sich somit:

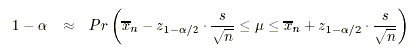
Und für den Stichprobenanteilswert:

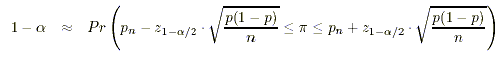
Vertrauensintervalle lassen sich ebenfalls grafisch darstellen. Dazu wurden in der unteren Darstellung dieselben Stichproben verwendet wie zur Darstellung von Mutungsintervallen.