5. Verteilung der Stichprobenanteilswerte
An dieser Stelle greifen wir noch einmal das Beispiel der Studierenden an der Universität Zürich auf, um das Konzept einer Stichprobenkennwerteverteilung anhand einer Computersimulation zu illustrieren.
Für die Population der Studierenden an der Universität Zürich ist die
Geschlechterverteilung bekannt: Im Wintersemester 2002/03 waren von der insgesamt
eingeschriebenen Studierenden 52,41% Frauen. Wir generieren also zunächst am Computer eine
Modellpopulation, welche das entsprechende Geschlechterverhältnis an der Universität
Zürich abbilden soll.
Zunächst soll gezeigt werden, dass aus unterschiedlichen Stichproben zum Teil sehr unterschiedliche Stichprobenanteilswerte resultieren. Aus den ersten fünf Zufallsstichproben vom Umfang n=500 resultierten die folgenden Werte für den geschätzten Frauenanteil:
| Stichprobe | Frauenanteil |
|---|---|
| Nr.1 | 49,8 % |
| Nr.2 | 52,8 % |
| Nr.3 | 53,2 % |
| Nr.4 | 53,8 % |
| Nr.5 | 52,2 % |
Zum Vergleich: Der tatsächliche Frauenanteil in der Population beträgt 52,41 %.
| Stichprobe | Frauenanteil |
|---|---|
| Uni ZH | 52,41 % |
Aus der Tabelle ist ersichtlich, dass für die ersten fünf Zufallsstichproben
jeweils ein anderer Anteilswert resultiert, und dass diese fünf Stichprobenanteilswerte
unterschiedlich nahe am tatsächlichen Populationsanteilswert liegen.
Wir führen
nun dieselbe Prozedur am Computer für 1'000 Zufallsstichproben mit jeweils einem
Stichprobenumfang von n = 500 durch. Stellt man die Verteilung der 500
Stichprobenanteilswerte grafisch dar, erhält man die Stichprobenverteilung des Anteilswertes.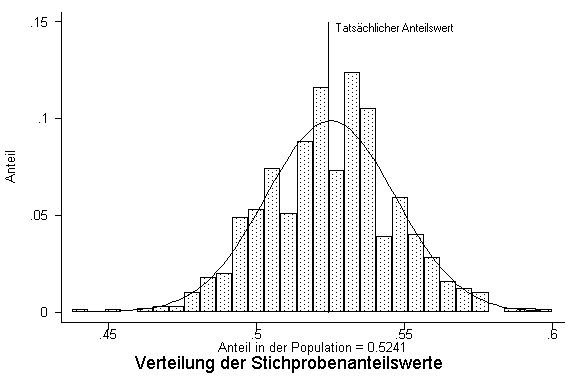
Aus der
Grafik wird folgendes ersichtlich:
- Die Verteilung der unterschiedlichen Stichprobenanteilswerte weist annähernd die Form einer Normalverteilung auf, wie die hinterlegte Normalverteilungskurve andeutet.
- Die unterschiedlichen Stichprobenanteilswerte sind um den tatsächlichen Populationswert von 52,41 % zentriert.
- Stichprobenkennwerte, welche "nahe" am tatsächlichen Populationskennwert liegen, sind wahrscheinlicher als Stichprobenkennwerte, welche "nicht nahe" am wahren Kennwert liegen. Wie der Grafik zu entnehmen ist, treten Stichprobenkennwerte kleiner als 0.45 oder grösser als 0.60 beispielsweise nur sehr selten auf.