Punktschätzungen für Populationsparameter liefern uns die bestmögliche Schätzung für den unbekannten Populationskennwert, wenn dieser aus Stichprobendaten geschätzt werden soll. Das Problem an Punktschätzungen ist allerdings, dass die mit der Stichprobenziehung verbundene Unsicherheit nicht berücksichtigt wird.
Wir wissen allerdings bereits, dass der Standardfehler eines Stichprobenkennwertes Auskunft über die Präzision gibt, mit welcher dieser Kennwert geschätzt werden kann. Mit dieser zusätzlichen Information lassen sich nun sogenannte Konfidenz- oder Vertrauensintervalle berechnen, welche im Gegensatz zu Punktschätzungen Auskunft über die Unsicherheit bezüglich dem Populationskennwert zum Ausdruck bringen.
Vertrauensintervalle lassen sich durch einfaches Umformen aus den entsprechenden Mutungsintervallen herleiten. Für den Stichprobenmittelwert ergibt sich folgende Formel für das Vertrauensintervall:

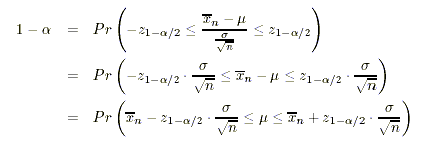
Für den Stichprobenanteilswert ergibt sich analog folgende Berechnung des Vertrauensintervalles:

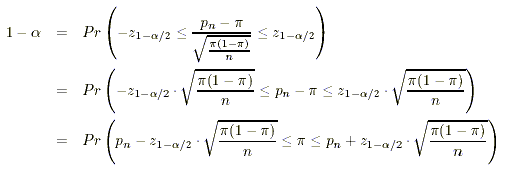
Wie lassen sich nun Vertrauensintervalle interpretieren? Vertrauensintervalle sind so konstruiert, dass sie mit einer vorgegebenen Wahrscheinlichkeit den tatsächlichen Populationskennwert umschliessen. Anders formuliert: Der unbekannte Populationskennwert befindet sich mit der vorgegebenen Wahrscheinlichkeit innerhalb des berechneten Vertrauensintervalles.
Die Breite des Vertrauensintervalles drückt aus, mit welcher Genauigkeit anhand der Stichprobe auf den Populationskennwert geschlossen werden kann. Die Breite des Konfidenzintervalles für den Stichprobenmittelwert bzw. -anteilwert ist gegeben durch den folgenden Ausdruck:

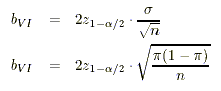
Anhand der obigen Formeln ist ersichtlich, welche Grössen die Breite des Vertrauensintervalles beeinflussen:

• Die Wahrscheinlichkeit, mit welcher das Vertrauensintervall den unbekannten Populationskennwert umschliessen soll. Je grösser diese Wahrscheinlichkeit sein soll, desto breiter wird das entsprechende Vertrauensintervall. Wollte man etwa ein Vertrauensintervall bilden, welches den wahren Populationskennwert mit 100% Wahrscheinlichkeit umschliesst, erhält man ein Vertrauensintervall von unendlicher Breite!
• Der Standardfehler des Stichprobenkennwertes. Je kleiner der Standardfehler des Stichprobenkennwertes, desto kürzer wird das Vertrauensintervall. Hier fliesst somit direkt die Präzision ein, mit welcher der Kennwert geschätzt werden kann.