Das zentrale Grenzwerttheorem ermöglicht es uns nun, Aussagen darüber zu formulieren, mit welcher Wahrscheinlichkeit ein Stichprobenkennwert innerhalb eines zentralen Wertebereiches zu erwarten ist, wenn aus der Population eine einzelne Stichprobe der Grösse n gezogen wird. Wir interessieren uns nun für die Wahrscheinlichkeit, dass ein (standardisierter) Stichprobenkennwert einer Zufallsstichprobe um + / - z Standardabweichungen vom tatsächlichen Populationskennwert entfernt ist. Wir stellen uns hier also die Frage, wie wahrscheinlich bzw. wie unwahrscheinlich konkrete Realisierungen von Stichprobenkennwerten sind, wenn wir eine einzelne Zufallsstichprobe aus einer bekannten Population ziehen (d.h. die Verteilung des Merkmales in der Population ist bekannt).

Einen solchen zentralen Wertebereich, innerhalb dessen der Stichprobenkennwert mit einer bestimmten Wahrscheinlichkeit zu erwarten ist, nennt man Mutungs- oder Prognoseintervall.

Ein Mutungsintervall für Stichprobenmittelwerte berechnet sich als:

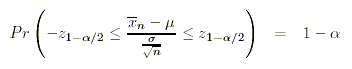
Ein Mutungsintervall für Stichprobenanteilswerte berechnet sich als:

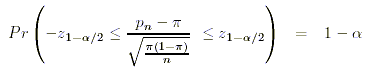
Mutungsintervalle besitzen somit folgende Interpretation: Beim Ziehen einer Zufallsstichprobe aus der Population beträgt die Wahrscheinlichkeit, dass der daraus berechnete Stichprobenkennwert innerhalb des Intervalles auf der linken Seite der Gleichung liegt, 1-alpha.

Vorgehensweise zur Bestimmung von Mutungsintervallen:

• Bestimmen Sie die gewünschte Wahrscheinlichkeit, mit welcher der Stichprobenkennwert innerhalb des Intervalles zu erwarten ist. Möchte man beispielsweise wissen, wie gross das Intervall ist, innerhalb dessen der Stichprobenkennwert mit einer Wahrscheinlichkeit von 90 % zu erwarten ist, ergeben sich die folgenden Grössen:
  

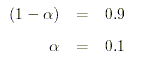
• Bestimmen Sie nun:

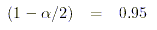
• Suchen Sie für diesen Wert den entsprechenden z-Wert der Standardnormalverteilung aus einer statistischen Tabelle oder bestimmen Sie diesen Wert am Computer.
  Für unser Beispiel sollten Sie den Wert 1,645 erhalten.
• Sie kennen nun bereits das zentrale Mutungsintervall.
  Für das Beispiel: 90 % aller z-transformierten Stichprobenkennwerte beim wiederholten zufälligen Ziehen einer Stichprobe werden sich im Intervall von + / 1,645 Standardabweichungen vom tatsächlichen Populationskennwert entfernt befinden.

Die z-Werte zu den wichtigsten Mutungsintervallen:

• 90 % aller Beobachtungen einer standardnormalverteilten Zufallsvariable liegen im Wertebereich von + / - 1,645.
• 95 % aller Beobachtungen einer standardnormalverteilten Zufallsvariable liegen im Wertebereich von + / - 1,96.
• 99 % aller Beobachtungen einer standardnormalverteilten Zufallsvariable liegen im Wertebereich von + / - 2,576

Grafische Illustration von Mutungsintervallen:

Das Konzept des Mutungsintervalles lässt sich grafisch illustrieren. Dazu wurde wiederum eine standardnormalverteilte Verteilung für eine Population von N = 10'000 am Computer generiert. Anschliessend wurden 100 Zufallsstichproben vom Umfang n = 500 aus dieser Population gezogen und der jeweilige Stichprobenmittelwert berechnet. In der folgenden Grafik sind die 100 Stichprobenmittelwerte und verschiedene Mutungsintervalle dargestellt.