Wie haben bereits gesehen, dass die Stichprobengrösse entscheidenden Einfluss auf den Standardfehler sowohl des Mittelwerts als auch des Anteilwertes ausübt. Der Einfluss der Stichprobengrösse soll nun anhand des Anteilwertes noch genauer illustriert werden, für den Mittelwert gelten allerdings analoge Ergebnisse.

Der Einfluss der Stichprobengrösse auf den Standardfehler des Anteilwertes lässt sich wiederum am einfachsten über eine Computersimulation zeigen. Dazu ziehen wir aus der Modellpopulation, welche die Geschlechterverteilung der Studierenden an der Universität Zürich abbildet, jeweils 1'000 Zufallsstichproben für unterschiedliche Stichprobengrössen.

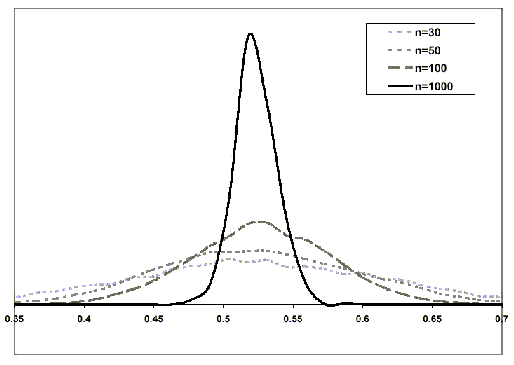
Anhand der Grafik ist deutlich zu erkennen, dass zwar alle Stichprobenverteilungen unabhängig vom Stichprobenumfang um den tatsächlichen Populationswert zentriert sind, dass aber mit steigendem Stichprobenumfang die Streuung der Stichprobenanteilswerte geringer wird. Mit steigendem n konzentriert sich somit die Stichprobenverteilung immer näher am wahren Anteilswert.

Der Zusammenhang zwischen der Stichprobengrösse und dem Standardfehler lässt sich auch noch auf eine andere Art und Weise illustrieren. Der Standardfehler des Anteilwertes ist gegeben durch die folgenden Grösse:

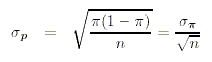
Die Populationsvarianz bzw. die Populationsstandardabweichung ist eine Konstante und lässt sich durch den Forscher in aller Regel nicht beeinflussen. Der Standardfehler variiert somit umgekehrt proportional zur Wurzel aus n. Der Zusammenhang zwischen dem Standardfehler und der Stichprobengrösse für das Beispiel der Geschlechterverteilung ist unten grafisch dargestellt:

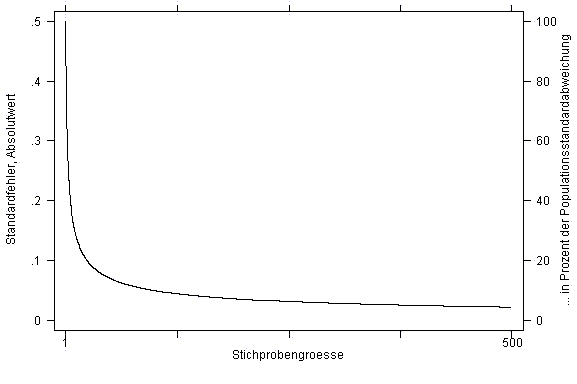
Zum einen ist der negative Zusammenhang zwischen der Stichprobengrösse und dem Standardfehler klar ersichtlich. Zum anderen zeigt sich, dass der Zusammenhang zwar monoton, aber nicht linear ist: Der Standardfehler "reagiert" zunächst sehr stark auf eine Vergrösserung der Stichprobe. Ist die Stichprobe bereits relativ gross, lässt sich durch eine weitere Vergrösserung der Stichprobe der Standardfehler nicht mehr markant verkleinern.

Aus diesem Ergebnis lässt sich der folgende Schluss ziehen: Will man als sozialwissenschafliche ForscherIn den Standardfehler reduzieren (und damit die Unsicherheit in Bezug auf den gesuchten Populationskennwert), sollte man um eine möglichst grosse Stichprobe besorgt sein, da man auf die Varianz des Merkmales in der Population keinen Einfluss nehmen kann.

Allerdings ist eine grosse Stichprobe alleine noch keine Garantie für eine präzise Schätzung des Populationskennwertes. Diese Präzision hängt ebenfalls entscheidend von der Art und Weise ab, wie die Stichprobe gezogen wurde. Weitere Informationen dazu finden Sie in einem separaten Lernschritt zur Stichprobenziehung.