Ohne mathematische Herleitung formulieren wir an dieser Stelle den bereits vorher beobachteten Sachverhalt:

Die Stichprobenverteilung über theoretisch unendlich viele Stichproben von Mittelwerten als auch von Anteilswerten folgt einer Normalverteilung - und zwar praktisch unabhängig von der Verteilungsform des Merkmales in der Population - falls die Stichprobe genügend gross ist. Diese Gesetzmässigkeit nennt man auch das zentrale Grenzwerttheorem.

Arithmetisches Mittel:

Die Stichprobenverteilung der Mittelwerte weist den folgenden Erwartungswert auf:

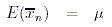
Das heisst, dass der Erwartungswert der Stichprobenmittelwerte dem tatsächlichen Populationsmittelwert entspricht. Dies bedeutet, dass die Stichprobenmittelwerte am wahren Populationsmittelwert zentriert sind.
Für die Varianz und die Standardabweichung der Stichprobenmittelwerte ergeben sich die folgenden Formeln:

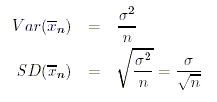
Die Standardabweichung der Stichprobenmittelwerte bezeichnet man auch als Standardfehler der Stichprobenmittelwerte. Der Standardfehler ist von zentraler Bedeutung, weil er ein Mass dafür ist, wie präzise ein Stichprobenmittelwert den unbekannten Populationsmittelwert schätzt. Aus obiger Formel ist ersichtlich, dass der Standardfehler lediglich von der Populationsvarianz sowie dem Stichprobenumfang abhängt. Insbesondere hat die Grösse der Population keinen Einfluss auf den Standardfehler.
Es gilt:

• Je grösser die Varianz des Merkmales in der Population, desto grösser ist der Standardfehler der Stichprobenmittelwerte. Bei konstanter Stichprobengrösse ist damit der Standardfehler umso grösser, je grösser die Populationsvarianz ist.
  Eine Stichprobe vom Umfang n schätzt damit den Populationsmittelwert umso besser, je weniger das Merkmal in der Population streut, d.h. je homogener die Beobachtungen in der Population sind.
• Je grösser der Stichprobenumfang, desto kleiner ist der Standardfehler. Auch dies sollte intuitiv sein, da mit steigendem Stichprobenumfang die Informationsunsicherheit über die Population reduziert wird. Im Extremfall von n = N wird der Standardfehler gleich Null, da in diesem Falle der Populationsmittelwert ohne Unsicherheit berechnet werden kann.

Anteilswert:

Für den Anteilswert erhält man analoge Ergebisse wie für das arithmetische Mittel. Der Erwartungswert der Stichprobenanteilswerte entspricht ebenfalls dem tatsächlichen Anteilswert in der Population:

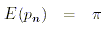
Die Varianz sowie die Standardabweichung der Stichprobenanteilswerte berechnen sich nach den folgenden Formeln:

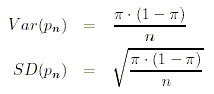
Auch hier gilt, dass der Standardfehler der Anteilswerte die Präzision umschreibt, mit welcher der Populationsanteilswert aus den Stichprobendaten geschätzt werden kann. Ebenso wie für den Mittelwert gilt auch hier, dass der Standardfehler nur von der Varianz der Merkmales in der Population sowie vom Stichprobenumfang abhängt.
Wiederum gilt:

• Je grösser die Varianz des Merkmales in der Population, desto grösser ist der Standardfehler des Anteilwertes. Dies bedeutet wiederum, dass eine Stichprobe vom Umfang n der Populationsanteilswert umso präziser schätzt, je homogener die Verteilung des Merkmales in der Population ist.
• Der Standardfehler sinkt mit steigendem Stichprobenumfang. Auch für den Anteilswert gilt somit, dass mit steigendem Stichprobenumfang der unbekannte Populationsanteilswert präziser geschätzt werden kann.

Exakte Verteilungsform der Stichprobenkennwerte:

Erwartungswert und Varianz bzw. Standardabweichung charakterisieren nun allerdings noch nicht die exakte Form der Verteilung der Stichprobenanteilswerte respektive der Stichprobenmittelwerte.
Gemäss dem zentralen Grenzwerttheorem weisen nun allerdings beide Verteilungen bei genügend grossem Stichprobenumfang eine Normalverteilung auf, welche durch die beiden besprochenen Grössen determiniert wird.
Damit kennen wir nun aber die exakte Verteilungsform sowohl der Stichprobenanteilswerte als auch der Stichprobenmittelwerte:

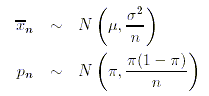
Inwiefern hilft uns nun aber diese Gesetzmässigkeit bei der Lösung des gestellten Problemes?
Wir machen uns zunächst die Tatsache zunutze, dass sich jede beliebige Normalverteilung in die Standardnormalverteilung überführen lässt. Dazu bilden wir die z-Werte unserer Stichprobenmittelwerte:

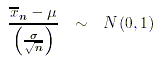
Beziehungsweise für die Stichprobenanteilswerte:

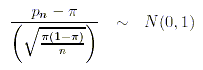
Die standardisierten Werte bringen somit zum Ausdruck, um wieviele Standardabweichungen ein Stichprobenmittelwert beziehungsweise ein Stichprobenanteilswert vom entsprechenden Populationskennwert entfernt ist.

Da wir nun die exakte Verteilungsform kennen, können wir eine Aussage darüber machen, wie wahrscheinlich oder eben unwahrscheinlich es ist, einen Stichprobenkennwert einer bestimmten Grösse zu beobachten.

Um beispielsweise die Wahrscheinlichkeit zu bestimmen, einen Stichprobenmittelwert zu beobachten, welcher 2 Standardabweichungen vom tatsächlichen Populationsmittelwert entfernt ist, muss man die Flächen links von z = -2 und die Fläche rechts von z = 2 unter der Standardnormalverteilung addieren.

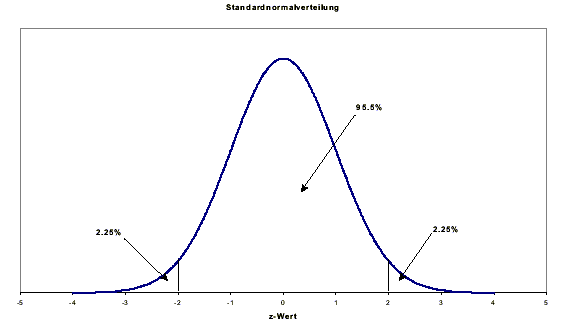
Sowohl die Fläche links als auch die Fläche rechts umfassen aufgrund der Symmetrie der Standardnormalverteilung jeweils ungefähr die Wahrscheinlichkeit von 2,5 %. Das heisst, die Wahrscheinlichkeit, dass sie einen Stichprobenmittelwert beobachten, welcher 2 oder mehr Standardabweichungen vom tatsächlichen Populationsmittelwert entfernt ist, beträgt nur ungefähr 5 %.