Da wir nun wissen, wie sich die Stichprobenkennwerte um den wahren Populationskennwert verteilen, können wir uns der praktisch relevanten Frage zuwenden, wie anhand einer einzelnen Stichprobe auf den Populationkennwert geschlossen werden kann, wenn dieser unbekannt ist (Zur Erinnerung: Bei der Berechnung von Mutungsintervallen geht man davon aus, dass die Populationskennwerte bekannt sind).

Zunächst stellt sich die Frage, wie der gewünschte Populationskennwert am besten aus den vorliegenden Stichprobendaten geschätzt werden kann. Solche Schätzungen für den Populationskennwert selbst nennt man auch Punktschätzungen.

Aus der Formulierung des zentralen Grenzwerttheorems wissen wir bereits, dass die Erwartungswerte der Stichprobenverteilung sowohl des Anteilwertes als auch des arithmetischen Mittels dem jeweiligen Populationskennwert entsprechen. Die besten Punktschätzer für diese beiden Kennwerte sind somit gegeben durch:

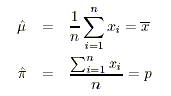
Die Varianz und die Standardabweichung des interessierenden Merkmales lässt sich anhand der folgenden Formeln schätzen:

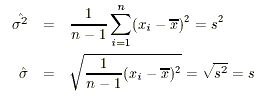
Punktschätzungen liefern uns zwar die besten Schätzungen für die unbekannten Populationskennwerte, sie geben uns aber keine Auskunft darüber, wie präzise diese Schätzungen sind.